Brief introduction to Convolutional Neural Networks

If you are reading this post, it means you know about convolutional neural networks (CNN) or you have heard about it before. But why should you read what I am offering you here? Indeed, there is a lot of documentation, tutorials, articles, and videos on this subject — often with complex mathematical notions that are difficult to understand. I read a lot on CNNs to understand part of it. It is a small and vast domain at the same time; once you understand the basics, leveling up becomes relatively straightforward.

At the end of the presentation, I will suggest two interesting resources to deepen or broaden your understanding.

Introduction

CNN is a type of Artificial Neural Network (ANN) used in image recognition and processing. It’s also widely used for video processing.

CNN process

A CNN sliding through a given matrix.

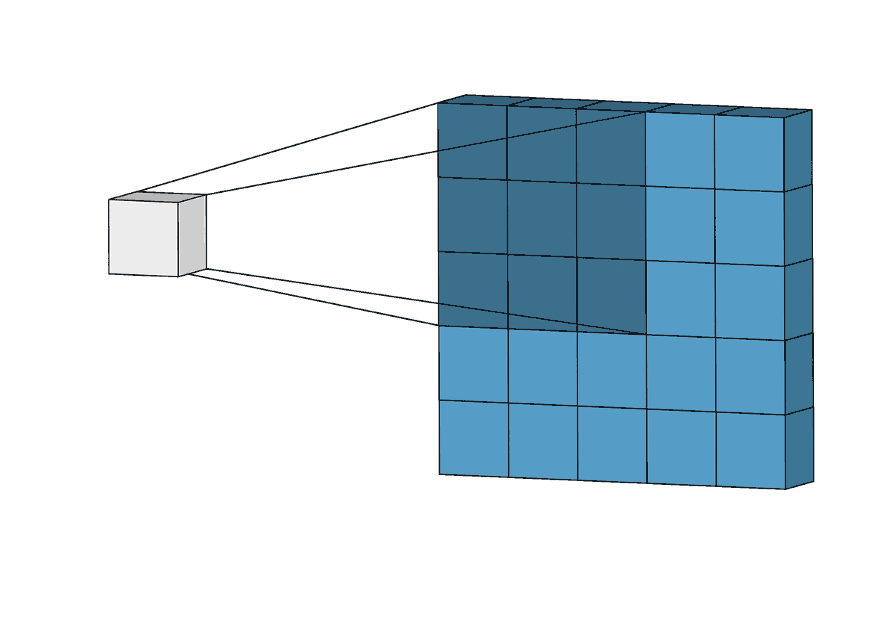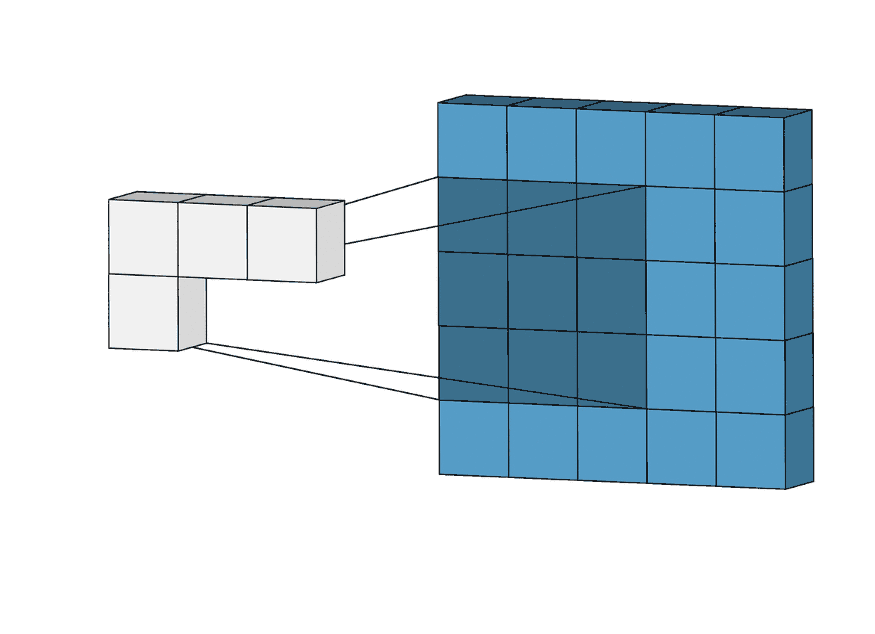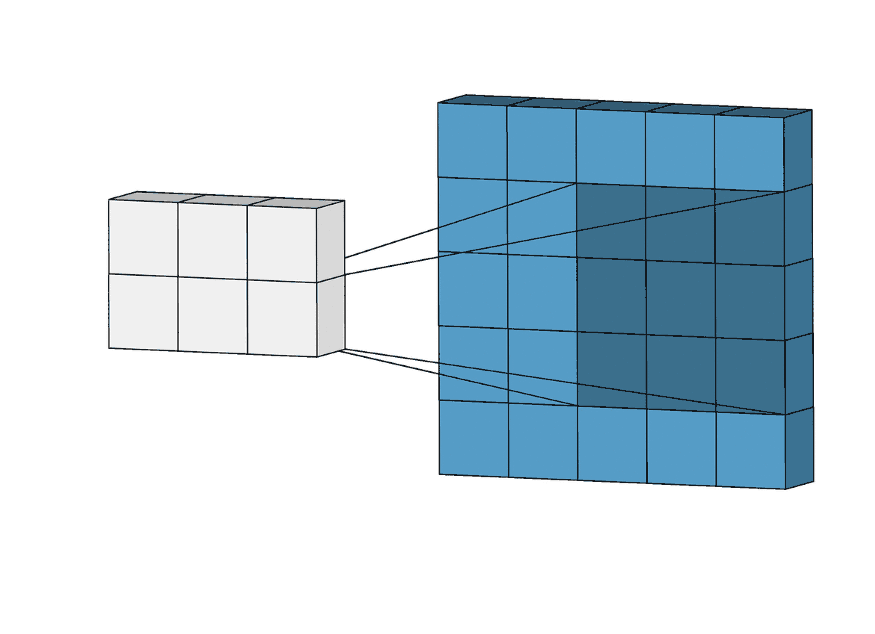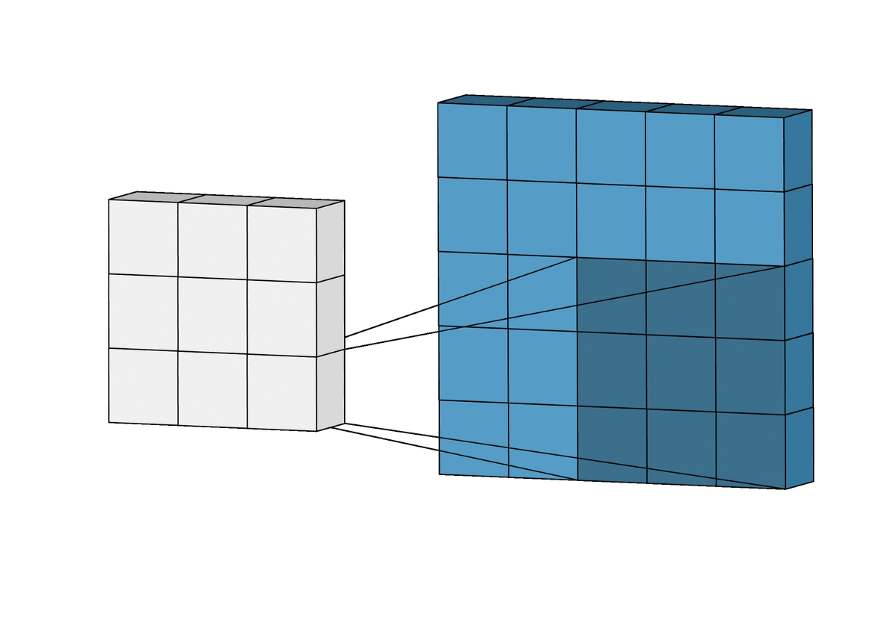
Convolution Layer

Suppose we have an input matrix \(X\) of dimension \(4 \times 4\):

\[\begin{split} X = \begin{bmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{bmatrix} \end{split}\]

To compute the convolution operation we need:

• Kernel size: refers to the dimensions of the sliding window over the input.

• Stride: indicates how many pixels the kernel should be shifted over at a time.

Let \(K\) be the associated kernel:

\[\begin{split} K = \begin{bmatrix} k_{11} & k_{12} \\ k_{21} & k_{22} \end{bmatrix} \end{split}\]

The convolution is computed as follows:

\[ Y_{1,1} = a \cdot k_{11} + b \cdot k_{12} + e \cdot k_{21} + f \cdot k_{22} \]

\[ Y_{1,2} = b \cdot k_{11} + c \cdot k_{12} + f \cdot k_{21} + g \cdot k_{22} \]

\[ Y_{1,3} = c \cdot k_{11} + d \cdot k_{12} + g \cdot k_{21} + h \cdot k_{22} \]

\[ Y_{2,1} = e \cdot k_{11} + f \cdot k_{12} + i \cdot k_{21} + j \cdot k_{22} \]

After the convolution operation, an activation function is applied.

See interactive explanation on CNN

Pooling

The aim of pooling is gradually decreasing the spatial extent of the network.

By using Max Pooling:

\[\begin{split} \max \left( \begin{bmatrix} 3 & 1 \\ 4 & 2 \end{bmatrix} \right) = 4 \end{split}\]

I intentionally left out the activation function, building a CNN (with PyTorch), etc. because the articles below talk about it very clearly. My objective here was to remove the complexity in the understanding of these two operations specific to CNNs.

From here take a look at this interactive explanation on CNN and the other article I’d like to introduce you is Convolutional Neural Networks, Explained

Thank you ☕!

Principal Component Analysis   La normalisation par lots

Comments

comments powered by Disqus